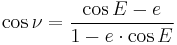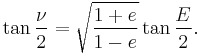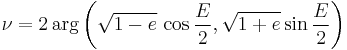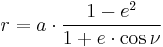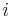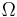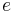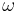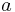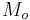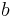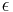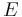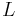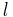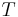True anomaly
In celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse (the point around which the object orbits).
The true anomaly is usually denoted by the Greek letters 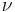 or
or 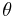 , or the Roman letter
, or the Roman letter  .
.
The true anomaly is one of three angular parameters ("anomalies") that define a position along an orbit; the other two being the eccentric anomaly and the mean anomaly.
Contents |
Formulas
From state vectors
For elliptic orbits true anomaly 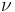 can be calculated from orbital state vectors as:
can be calculated from orbital state vectors as:
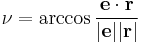 (if
(if 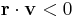 then replace
then replace 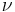 by
by 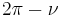 )
)
where:
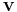 is orbital velocity vector of the orbiting body,
is orbital velocity vector of the orbiting body,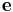 is eccentricity vector,
is eccentricity vector, is orbital position vector (segment fp) of the orbiting body.
is orbital position vector (segment fp) of the orbiting body.
Circular orbit
For circular orbits the true anomaly is undefined because circular orbits do not have a uniquely determined periapsis. Instead one uses the argument of latitude u:
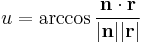 (if
(if 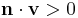 then replace
then replace 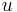 by
by 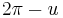 )
)
where:
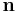 is vector pointing towards the ascending node (i.e. the z-component of
is vector pointing towards the ascending node (i.e. the z-component of 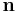 is zero).
is zero).
Circular orbit with zero inclination
For circular orbits with zero inclination the argument of latitude is also undefined, because there is no uniquely determined line of nodes. One uses the true longitude instead:
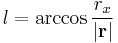 (if
(if 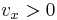 then replace
then replace 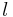 by
by 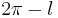 )
)
where:
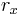 is x-component of orbital position vector
is x-component of orbital position vector 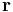 ,
,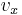 is x-component of orbital velocity vector
is x-component of orbital velocity vector 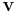 .
.
From the eccentric anomaly
The relation between the true anomaly 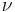 and the eccentric anomaly E is:
and the eccentric anomaly E is:
or equivalently
Therefore
where 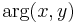 is the polar argument of the vector
is the polar argument of the vector 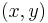 (available in many programming languages as the library function atan2(y, x), beware that the arguments are usually in reversed order).
(available in many programming languages as the library function atan2(y, x), beware that the arguments are usually in reversed order).
Radius from true anomaly
The radius (distance from the focus of attraction and the orbiting body) is related to the true anomaly by the formula
where a is the orbit's semi-major axis (segment cz).
See also
References
- Murray, C. D. & Dermott, S. F. 1999, Solar System Dynamics, Cambridge University Press, Cambridge.
- Plummer, H.C., 1960, An Introductory treatise on Dynamical Astronomy, Dover Publications, New York. (Reprint of the 1918 Cambridge University Press edition.)